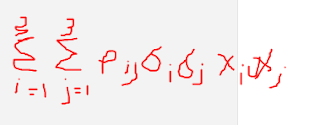LM5001
################################## START 20150614 ###############################
Introduction
Optimization Model
Excel Solver
Add Excel solver
https://support.office.com/en-nz/article/Load-the-Solver-Add-in-612926fc-d53b-46b4-872c-e24772f078ca
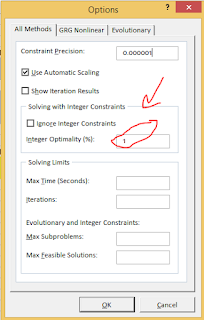
ปัญหา Solver ไม่ยอดคิดเป็น Interger ให้ปรับ Ignore Integer Constrain ออก ที่ Option ดังนี้
การ Ignore Integer Constrain จะทำให้เราไม่สามารถ Output Sensitivity Report ได้นะครับ ถ้าจะใช้ต้องปรับกลับเป็นค่าเดิมด้วย
โจทย์ 13.2 (P.661)
การเขียน Objective Function
ให้ x1 แทนปริมาณ Basic ที่จะผลิตในเดือนหน้า
ให้ x2 แทนปริมาณ XP ที่จะผลิตในเดือนหน้า
เขียน Decision Variable
5x1 + 6x2 <= 10,000
x1+2x2 <= 3,000
x1 <= 600
x2 <= 1,200
x1,x2 >= 0
Constrain
- Binding constrain คือเครื่องหมาย = มีผลต่อ Objective function เป็นส่วนที่สำคัญเช่นถ้าเรามีค่าที่เปลี่ยนไป จะต้องเปลี่ยน Objective Function ใหม่ เช่น จ.น. ชม ลดลงจาก 3000 เป็น 2999 จะต้องเปลี่ยน OF ใหม่ทันที
- Non-Binding Constrain คือเครื่องหมาย อื่นๆ นอกจาก = เช่น <=, >= เป็นส่วนที่ไม่สำคัญ เช่น จ.น. ชม. เพิ่มขึ้น จาก 3,000 ชม. เป็น 3010 ก็ไม่ได้ทำให้ผลกำไรเพิ่มขึ้น ดังนั้นถ้าเราจะหาแรงงานเพิ่ม เราควรหา แรงงานในส่วน Assembly เพิ่มขึ้น แทนมากกว่า
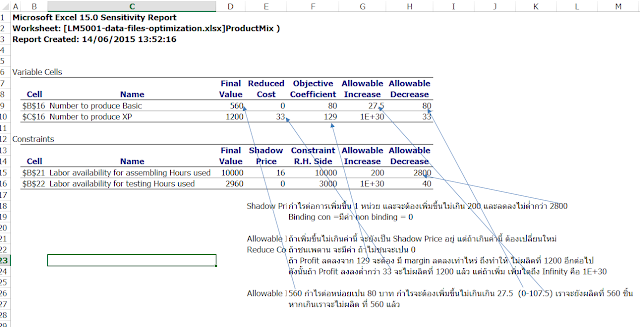
Sensitivity (จะมีอะไรเปลี่ยนไปถ้า Input เปลี่ยนไป
คุณสมบัติที่สำคัญของการเป็น
Linear Programming
- proportionality (การเพิ่มขึ้น / สัดส่วน)
- addivity (กำไรของ xp + กำไรของ basic ได้)
- divisibility
Integer Programming
ถ้า เป็น Integer เราจะต้อง define ให้ decision variable เป็น จำนวนเต็ม จะเรียกว่า Integer Programming
proportionality + addivity จะไม่มีการ ยกกำลัง
ซึ่งจะต้องอยู่ในรูปแบบนี้เท่านั้น ax + by + cz + .... จะต้องเปนทั้ง constrain + objective function ด้วย
การแก้ปัญหา แล้วไม่ได้มี 2 แบบ
- Infeasible
- Unboundedness
Feasibility =
Solution ที่สอดคล้องกับ Constrain
Infeasible = Region เปน empty set
Feasible Region (fr) = Region ที่สอดคล้องกับ Constrain
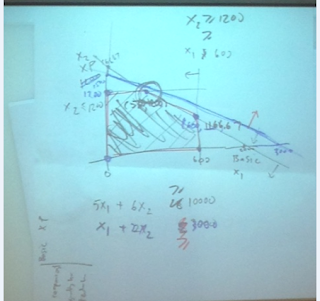
Unboundedness
ถ้า objective เราคือ minimize unbound คือ เราสามารถทำให้ cost ต่ำลงจน infiity ได้
fr
Infeasible เกินจาก เราอาจใส่ constrain มากเกิน
Unbounded ลืมใส่ constrain เลยผลิตไปได้เรื่อย ไม่มีทีสิ้นสุด
Continue --------
โจทย์ อยู่ในหนังสือ บทที่ 13.3
การเขียน Objective Function
xt = ปริมาณลูก foot ball ที่ผลิตในเดือน t เมื่อ t = 1-6
It = inventory ปลายเดือน t เมื่อ t = 1-6
Minimize Cost = (12.5*x1 + ... + 12.95*x6) + (0.05*12.5*I1 + ... + 0.05*12.95*I6)
หรือ
Subject To : (Constain)
กำหนด ให้
I0 = 5,000
x1 <= 30,000
.
.
.
x6 <= 30,000
หรือเขียนว่า
xt <=30,000 ; t=1,2,..,6
It <= 10,000 ; t=1,2,...,6
5000 + x1 >= d1 หรือ I0 + x1 >= d1
I1 + x2 >= d2
I2 + x3 >= d3
หรือเขียนว่า
It-1 + xt >= dt ; t=1,2,...6
xt >= 0
เขียน Decision Variable
กำหนดให้
d1 = 10000
d2 = 15000
d3 = ....... d6 (ดูในตาราง)
I1 = (5,000 + x1) - 10,000 = (5000 + x1) - d1
I2 = (x1 + x2) - d2
.
.
.
I6 = (x5 + x6) - d6
A Seven -Step Modelling Process
1. วางปัญหา จะ minimize cost หรือไม่ อะไรเปน contrain ข้อจำกัดอะไร อยากจะตัดสินใจอะไร
2. เกบข้อมูล production / warehouse
3. สร้าง model
4. Verify model : เวลาเราได้ spread sheet เราน่าจะเอาแผนการผลิตที่ผ่านมา ใส่เข้าไป แล้วดูว่าค่าใช้จ่ายใกล้เคียงกับที่เกิดขึ้นจริงไหม เพื่อเปนการ verify ว่า verify มันถูกหรือไม่
5. เลือกการตัดสินใจที่เหมาะสม
6. เสนอ
7. update กรณีมีสิ่งแวดล้อเปลี่ยนไป
################################### END 20150614 #################################
################################### END 20150621 #################################
Chapter 14
Logistics Model
ต้นทาง มีหลาย Org หลาย Dest อาจจะเปนโรงงาน กับ Retial / WH / Cust
Ex Factory to Retial แต่ละโรงงานจะต้องมี capa ว่าแต่ละโรงงานผลิตได้กี่ชิ้น
ดังนั้นของที่จะส่ง จะต้องไม่เกินโรงงานที่ผลิตได้ (Contraint)
Retailler จะมี demand ในสัปดาห์นี้จะต้องส่งขอให้ได้ กี่ชิ้น จะเรียก
Demand Node / Supply node
Objective F ทำยังไงให้ต้นทุนขนส่งรวม ต่ำที่สุด
โจทย์ EXP 14.3 (P.734)
Desision Variable = Plant(3) x Region(4) = 14 DV
X11 ปริมาณ รถ ที่ขนจาก p1 ไป r1
X12 p1 ไป r2
.
.
X34 p3 ไป r4
เขียนสั้นๆให้
= > Xij = ปริมาณที่สนส่งจาก plant i ไป region j โดยที่
i = 1,2,3
j = 1,2,3,4
Obj F
min 131X11 + 218X12 + .... 180X34
Constrain
- ของที่ออกจากแต่ละโรงงานต้องไม่เกิน Capacity
X11 + X12 + X13 + X14 <= 450
X21 + X22 + X23 + X24 <= 600
X31 + X32 + X33 + X34 <= 500
X11 + X21 + X31 >= 450
X12 + X22 + X23 >= 200
X13 + X23 + X33 >= 300
X14 + X24 + X34 >= 300
Xij > = 0 ; i=1,2,3 j=1,2,3,4
เราสามารถเปลี่ยนมิติ แล้วใช้ Sum if ช่วยก็ได้
&SUMIF (ArrayValue,Target_Value,SumValue)
ความหมาย รวมค่าใน SumValue ของ Table ที่ตรง กับ ArrayValue = Target_value ที่เลือก
Feasible Solution Image
END
Node ที่มีทั้ง Inflow และ Outflow เรียกว่า Transhipment Point.
ที่ Transhipment จะเอา Inflow - Outflow = net inflow // Outlfow - Inflow = net outflow
inflow - outflow = 0 หมายความว่า inflow = outflow
หรือ net outflow = 0 หมายความว่า outflow - inflow = 0 = > outflow = inflow
ถือเปน Constrain ที่ Transhipment point
โจทย์ EXP 14.4 (P.742)
Obj F minimize cost
5X12 + 3X13 + .... + 7X76 = Cost
DV = 26 ตัว
Constrain
(X12 + X13 + X14 + X15 + X18 + X17) - (X21+X31) <= 200 (Outflow - Inflow (Net Outflow) ไม่น้อยกว่า Capa)
(X21 + X23 + X24 + X25 + X26 + X27 ) - (X12 + X32) <= 300
.
(X14 + X24 + X34 + X54) - (X45 + X46 + X47) = 0 (Inflow = Outflow)
(X15 + X25 + X35 + X45) - (X54 + X56 + X57) = 0
(X16 + X26 + X36 +X46 +X56 + X76) - X67 >= 400 (Demand In - Out (Net Inflow) มากกว่าที่ต้องการ)
(X17 + X27 + X37 + X47 + X57 +X67) -X76 >= 180
0 <= Xij <= 200 (แต่ละเส้นทาง ขนส่งได้ไม่เกิน 200 หน่วย)
Assignment 14.25 ส่งอาทิตย์หน้า
ช่วงบ่าย
Integer Programming
แบ่งได้ เปน 2 อย่าง
- Special case ที่ DV เปนได้แค่ 0-1 จะเรียกว่า Binary Variable
- Normal case ตามปกติ
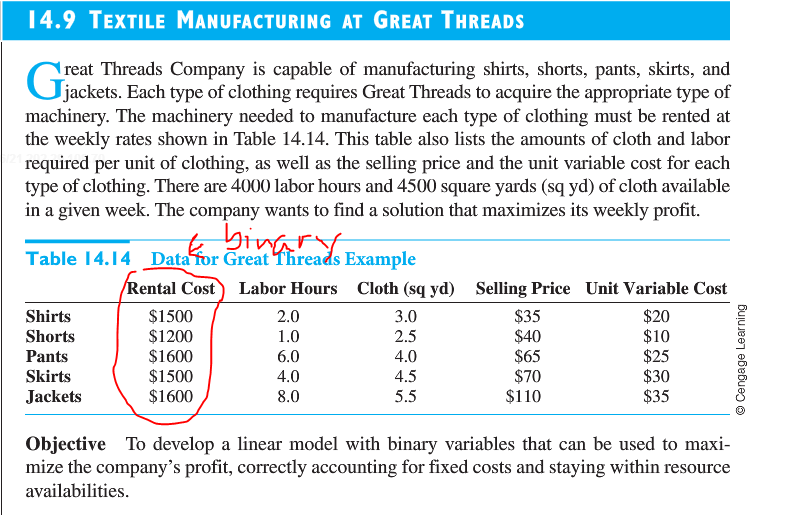
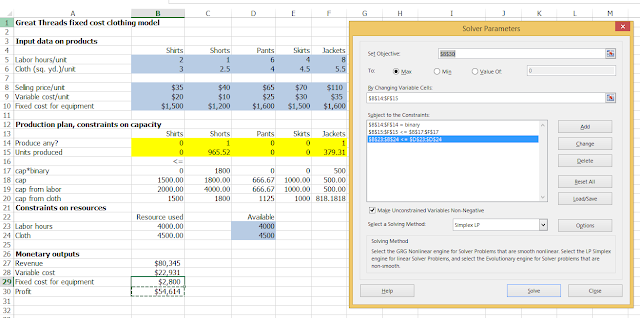
โจทย์ 14.9 (P.776)
DV
X1 = ปริมาณ ผลิต Shirt
X2 = ปริมาณ ผลิต Short
X3 = ปริมาณ ผลิต Pant
X4 = ปริมาณ ผลิต Skirt
X5 = ปริมาณ ผลิต Jacket
Y1 = 1 ; มีการผลิต Shirt / 0 ; ไม่มีการผลิต Shirt
Y2 = 1 ; มีการผลิต Short / 0 ; ไม่มีการผลิต Short
Y3 = 1 ; มีการผลิต Pant / 0 ; ไม่มีการผลิต Pant
Y4 = 1 ; มีการผลิต Skirt/ 0 ; ไม่มีการผลิต Skirt
Y5 = 1; มีการผลิต Jacket / 0 ; ไม่มีการผลิต Jacket
Obj F = Max ((35-20)X1 + (40-10)X2 + ... + (110-35)X5) - (1500Y1 + 1200Y2 + ... + 1600Y5)
Constrain
2X1 + X2 + ... + 8X5 <= 4000
3X1 + 2.5X2 + ... + 5.5X5 <= 4500
Yj = 0 --> Xj = 0
Xj > 0 --> Yj = 1
X1 <=
1500Y1
X2 <=
1800Y2
X3 <=
666.67Y3
X4 <=
1000Y4
X5 <=
500Y5
Xj >= 0, Yj = 0,1 ; J = 1-5
ในการคิด Mj จะต้องใช้ปริมาณ ที่สูงที่สุด เท่ากับ Constrain ที่มีมากำหนด เช่น ถ้าชม.การผลิต มี 4500 แล้ว ผ้ามี 4000 จะผลิต Shirt จาก เงื่อนไขนี้ ได้มากที่สุดกี่ตัว ให้เป็น Mj
โจทย์ (P.788) เพิ่มข้อก่อนหน้า
Recognizing the Optimal Integer Solution Effect of solver Tolerance Setting
ถ้ามัน Solve นาน เราอาจจะยอมให้อยู่ใน Range เป็น % ที่ยอมรับของ Optimal ก็ได้
ตามปกติ เวลา Solve Excel จะแสดง "incumbent" solution มาให้ในเวลาไม่กี่วิ เราอาจจะเลือกค่านี้เลยก็ได้ จะได้ไม่ต้องรอ นาน
END
Portfolio Optimization Models
Asset allocation = มีทรัพยากรอย่างจำกัด เราจึงต้องหา Optimize เพื่อให้เกิดประโยชน์สูงสุด
Constrain
X1 + X2 +X3 = 1 ----------------------------- 1
Mean return -->
.14X1 + .11X2 + .10X3 หรือ u1X1 + u2X2 + u3X3
อยากเลือกว่าจะลงทุนอย่างไรเพื่อให้ได้ความเสี่ยงต่ำสุด และได้ผลตอบแทนเฉลี่ย อย่างน้อย 12%
u1X1 + u2X2 + u3X3 >= 0.12 -----------------------------2
Risk = Variance (Std^2)
เขียนให้ ง่ายๆ คือ
i=1 , j = 1,2,3 -- > p11q1q1x1x1 + p12q1q2x1x2 + p13q1q3x1x3
i=2 , j = 1,2,3 --> p21q2q1x2x1 + p22q2q2x2x2 + p23q2q3x2x3
i=3 , j = 1,2,3 --> p31q3q1x3x1 + p32q3q2x3x2 + p33q3q3x3x3
Obj F
min q1^2 x1^2 + q2^2 x2^2 + ... + ก้อน ข้างบน
ไม่ได้ Solve ใน Excel นะ อ.ไม่ได้ทำให้ดู แค่บอกว่าใช้ โปรแกรมอื่นได้ เช่น ampl ดูได้ใน link
http://ampl.com/products/ampl/
https://en.wikipedia.org/wiki/List_of_optimization_software
อาทิตย์หน้า donwload R มาลงในเครื่องด้วย
http://www.r-project.org/
################################## END 20150621 ###############################
################################## START 20150628 ###############################
Data Analysis P.25
Type of Data
Numerical
Time Series = เวลาผ่านไปเก็บ 1 ครั้ง หลายๆ ครั้ง
Cross-Sectional = เก็บที่ Point เดียวในแต่ละเวลา
Categorical
Ordinal = เรียงได้ เช่น ลำดับ
Norminal = เรียงไม่ได้ เช่น ศาสนา
Dumny = 0,1
เราสามารถทำให้ Numerical เป็น Categorical ได้
เช่น Age เปลี่ยนเปนช่วง เช่น Age = 35 -> Middle-aged , 0 -> Young , 60 - > Elderly
&VLOOKUP ( Target Value, Array,Column_Index) || Ex Opinion
ความหมาย หาค่าที่ ตรงกับ TargetValue จาก Array ของ Table นี้ค่าใดๆที่ปรากฏ โดยถ้าปรากฏ ให้นำค่าใน Column_Index มาแสดง
ถ้าขึ้น #N/A = Not Application หาค่าไม่เจอ อาจเป็นเพราะ Range ที่เราใส่ไว้ไม่คลุมค่าทั้งหมด
&COUNTIF (Array,Target_Value)
ความหมาย นับค่าใน Array ของ Table ที่ตรง กับ Target_value ที่เลือก
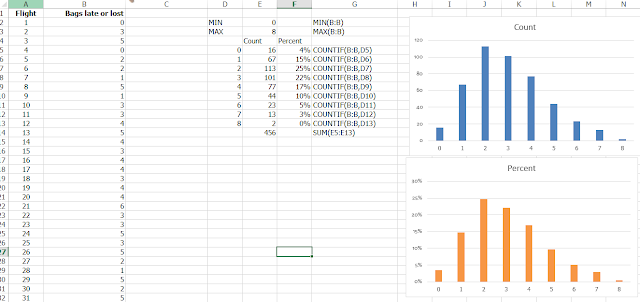
P.27 การใช้สูตร Count if และการหา Percentage
P.31 การ หา Mean Median Mode Range Varience Stdev
&MEAN(ValueList)
Mean : ค่าเฉลี่ยของทุกๆ ค่า (ข้อเสีย ถ้ามีค่าที่โดด เกินไปจะทำให้ Mean ที่ได้ไม่ถูกต้อง)
ถ้าเราใช้ในการดูข้อมูลพวกค่ากลางของเงินเดือน เราไม่ควรดูที่ Mean อย่างเดียว
&MEDIAN(ValueList)
Median : นำค่ามาเรียงกันจากมากไปหาน้อยแล้วเอาค่าตรงกลาง สามารถใช้ดูค่ากลางได้ดีกว่า Mean
&MODE(ValueList)
Mode : ค่าที่เกิดขึ้นบ่อยที่สุด
&MIN(ValueList) หาค่าต่ำสุดในช่วง
&MAX(ValueList) หาค่าสูงสุดในช่วง
Range : พิสัย : ค่าสูงสุด - ค่าต่ำสุด (ถ้า พิสัยเป็น 0 หมายความว่ามีตัวเลขที่ค่าเดียว)
&VAR.P(ValueList)
&VAR.S(ValueList)
Variance : ค่าความแปรปรวน หรือ กำลัง 2 ของ ส่วนเบี่ยงเบนมาตรฐาน
มี 2 แบบ Var.s ความแปรปรวนของกลุ่มตัวอย่าง Sample
Var.p ความแปรปรวนของประชากร Population
&STDEV.S(ValueList)
&STDEV.P(ValueList)
Standard Deviation : ส่วนเบี่ยงเบนมาตรฐาน
มี 2 แบบ Stdev.s ส่วนเบี่ยงเบนกลุ่มตัวอย่าง Sample
stdev.p ส่วนเบี่ยงเบนกลุ่มประชากร Population
STD
จะบอกการกระจายตัวของข้อมูล
Ex
SP1 Mean = 100 cm ,STD = 3 cm
: 68% ของค่าทั้งหมดจะอยู่ในค่า Mean +- STD (100-3) อยู่ระหว่างค่า 97 - 103
: 95% ของค่าทั้งหมดจะอยู่ในช่วง Mean^2 +- STD ^2 อยู่ประหว่างค่า 94 - 106
: 99.7% ของค่าทั้งหมดจะอยู่ในช่วง Mean^3 +- STD ^3 อยู่ประหว่างค่า 91 - 109
การวัด ให้ SP ส่ง Sample มา 100 อัน เราก็วัด Diameter
โอกาศ ที่เค้าจะผลิตออกมาแล้วได้ 115 cm น้อยมาก
โอกาศ ที่เค้าจะผลิตออกมาแล้วได้ 103 cm ค่อนข้างเยอะ
P.47 การ หา Mean Median Mode Range Variance Stdev
กราฟ นี้เบ้ขวา
การแจกแจง สมมาตร จะมี
Mean , Median , Mode เท่ากัน
Histrogram and Skewness
แกนตั้งเปน Frequency
แกนนอนเปน ข้อมูล
เบ้ ขวา mean > median
เช่น ประกันอุบัติเหตุ ส่วนมากจาก น้อย เพราะฉะนั้น กราฟจะเบ้ ขวา
เช่น ทรัพย์สิน ประชากร เบ้ ขวา
เช่น ระยะวันที่เสร็จงานของผู้รับเหมาสร้างบ้าน เวลาส่วนมาเสร็จ 4 เดือน ส่วนมากเสร็จภายใน 4 เดือน แต่ส่วนน้อยอาจจะล่าช้า
เบ้ ซ้าย mean < median
อ.ไม่ได้ยกตัวอย่าง
นอกจากจะวัดเปน Histogram เราสามารถใช้ Skewness วัดได้
&SKEW(ValueList)
ถ้ามีค่าเป็น + จะเป็นเบ้ ขวา
ถ้ามีค่าเป็น - จะเปนเบ้ ซ้าย
ถ้ามีค่าเป็น 0 จะเป็น Symmetric
จาก ตัวอย่าง Baseball = Skewness = 2.10 คือเบ้ ขวา ส่วนน้อยมีเงินเดือนเยอะ
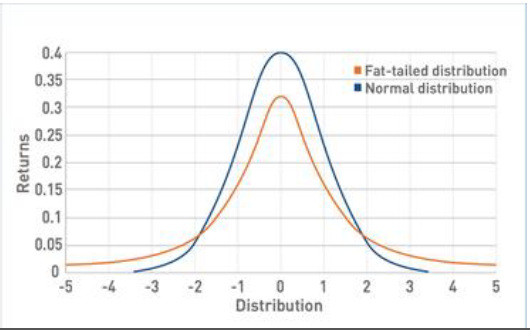
Kurtosis (อ.ไม่ได้เน้น นะ)
ความอ้วน ของกราฟ
มี fat tail (เส้นสีแดง) มีข้อมูล สูงหรือต่ำมากๆ (Extreme Value) เกิดขึ้นได้บ่อย
&KURT(ValueList)
ค่ามาก มี Fat-tailed มาก
นอกจากนี้ยังมี Blog plot
Mean คือ Percentile ที่ 50
ถ้า Percentile ที่ 75 หมายความว่า จำนวนของคนที่ได้คะแนน น้อยกว่าเท่ากับ 75%
Percentile 25 = 1st Quartile ( ดูรูปด้านบน)
เช่นถ้ามี คน 1000 คน 1st Quartile ได้ 37 หมายความว่า มีคนอยู่ทั้งหมด 250 คนได้คะแนนน้อยกว่า 37 คะแนน
Percentile 75 = 3rd Quatile
Inter Quatile Range (IQR) = 3rd Quatile - 1st Quatile
ถ้าได้เยอะแสดงว่าข้อมูลกระจายเยอะ
Upper Whisker = 1.5 เท่า ของ Interquatile range เป็น Observation สุดท้าย ที่อยู่ไม่เกิน 1.5 เท่า
อะไรก็ตามที่อยู่นอกหนวด
Mild Outlier = Out นิดๆ
Extreme Outlier = Out เยอะๆ
สามารถ เขียนกราฟได้ดังนี้
ตัวอย่างจาก Baseball
ช่วงบ่ายย
การเลือกใช้กราฟ
การหา Relationship ของข้อมูล
ตัวอย่าง P.83 Smoking And Drinking
ข้อมูลพวก Categorical ทำได้แค่นับ เท่านั้น
อ.ไม่ได้อธิบายความหมายให้นะครับ
P.95 Golf
ไม่มีความสัมพันธ์กัน
แต่หากเห็นเป็น Trend จะถือว่ามีความสัมพันธ์กัน
การหาก ความสัมพันธ์กันมากน้อยแค่ไหน โดยใช้
Correlation and Covariance
การหาก Collelation ใน Excel
&CORREL(ValueList,ValueList2)
ความสัมพันธ์ระหว่าง Yards/Drive vs Accuracy มีความสัมพันธ์ เชิงลบ
##สามารถ ใช้ Stat Tools สร้าง Correlation Metrix ได้ด้วยนะ (ถามเพิ่มเฉยๆ)
วิเคราะห์ Trend line ระหว่าง Yard vs Accuracy
ถ้า accuracy เพิ่มขึ้น 1 หน่วย yard จะลดลงเท่าไหร่
หลังจาก plot แล้ว ให้ add trend line มันจะให้ สมการมา เราจะรู้ได้ว่า
ถ้า driving acc เพิ่ม 1 หน่วย yard จะลดลง -1.0623 หน่วย
กราฟจากการทำ Excel
การใช้ Pivot Table
P.108
- เลือกที่ Data -> Insert -> Pivot Table
- ปรับ Dimension ตามนี้ อย่าลืมปรับ Properties ตรง Values เป็น Sum ด้วย
Tableau desktop เจ๋งเว่อ
ตัวอย่าง R การทำ Box Plot
- Open Program
- Load File
d <- read.table("R.txt",head=T,sep="\t")
พิมพ์ d จะสามารถดูข้อมูลได้
คำสั่งที่สามารถใช้ได้ใน R
mean(d$Salary)
summary(d$Salary)
boxplot(d$Salary~d$Position)
รูปด้านล่าง คำสั่ง Boxplot
สอบ
- Optimization (บทที่ 13,14) ไม่ออก บรรยาย
- Sensitivity ออกด้วย
- ตัวอย่าง การผลิต มี model 2 model วางแผน 1 เดือน
- ตัวอย่าง มี product เดียว แบบ pig skin วางแผนล่วงหน้า 6 เดือน พยายาม minimize cost ที่พูดถึงใน pig skin (holding cost) , Production Cost, เกี่ยวกับ Inventory สำคัญมากต้องทำ Excel ให้ได้
มี Constrain ต้องตอบสนอง demand
- Propertie อะไรแปลว่าอะไร ไม่ออก
- Integer Programming (0-1) ใช้ใน Model ตั้งแต่ง่ายสุด เช่น เลือกไม่เลือก ตั้งไม่ตั้ง หรือใช้ในกรณีที่มี fix cost เช่น ตัด ผ้า แล้วมีค่าเช่าเครื่องจักร ไม่ขึ้นอยู่กับปริมาณการผลิต เวลาคิดจะต้องเอา fix cost คูณกับ Binary , มี constrain ที่บอกว่า binary ต้องมากกว่า 0
- non linear ไม่ออก
- Transportation ไม่ออก
ข้อสอบมี 4 หน้า
คะแนน
40 - 40 - 20 Mid,Final,Homework
################################# START 20150717###############################
ไม่ได้ลงเนื้อหา
กรณีที่มีความไม่แน่นอน Uncertainty เราจะตัดสินใจ อย่างไร
มี 2 แบบ
- exact probability model
เราต้องทราบว่าสิ่งที่ไม่แน่นอน มี distribution แบบได ได้แก่ Normal + Binomial
- simulation ตัวอย่างการโตของเศษรฐกิจ
################################ END 20150717 ##################################
################################# START 20150726###############################
Simulation Model
ตัวอย่างโปรแกรม Discrete - Event Simulation = Arena , Simio ใช้ในกรณีเช่นร้านกาแฟ มีประเภทลูกค้าเข้ามา หลายแบบ เช่นซื้อแล้วออก ซื้อแล้วนั่ง ซื้อแล้วทำธุรกิจด้วย , เวลาที่ใช้ในการ ทำกาแฟ , จำนวน Server คนที่ทำกาแฟ เปนเหตุการต่อเนื่อง ฯลฯ
- การทำ Simulation จะทำให้เห็น Output ทำให้เราเห็นเหตุการที่เป็นไปได้ทั้งหมด ดีสุดแย่สุด
- ช่วยตอบคำถาม โดยไม่ต้องไปทำจริง (ไม่ต้องไปเปลี่ยนระบบจริง)
การจะทำ คือ ทำเมื่อมีความไมม่แน่นอน
เราจะต้องเลือก Distribution ให้เหมาะสมโดย วิเคราะห์จากข้อมูลในอดีต โดยไปเทียบกับข้อมูลทางสถิติ
การเลือก Distribution
- Discrete ค่าที่เปนไปได้ ได้แก่ 0 1 2 3 (เช่น จำนวนลูกค้า)
- Continutous ค่าที่มีทศนิยม (เช่น ปริมาณน้ำฝน)
- Symetric หรือ Skew เปนสมมาตร หรือแบบ เบ้ซ้ายขวา
Symetric
Skew
เช่น คนใช้เวลาในธนาคาร ส่วนใหญ่จะใช้เวลาแปบเดียว
- Bounded / Unbound คือมีค่าต่ำสุด หรือสูงสุด เช่น เวลาที่ น.ศ. ใช้ทำข้อสอบ Upper = 180 Min Lower = 30 Min
- Nonnegative / Unrestricted เช่น ปริมาณน้ำฝน เปนค่า + อย่างเดียว ถ้าเปนผลตอบแทนจากหุ้น อาจจะติด - ได้
บทที่ 15 (P 812)
Ex 15.1 (P 834)
ดูเรื่องระดับการให้บริการ
เราควรจะสั่ง ทำปฏิทิน มาเท่ากับ 200 อัน เลยดีไหม (Mean = 200) จากโจทย์
ตอบ ไม่ดี มันจะมีโอกาศที่ ไม่มีของ มีสูงถึง 50% การแจกแจงปกติ
P(D>200) = 0.5
ดูเรื่อง Cost
กำไรถ้าขายได้ 2.5
ถ้าขายไม่ได้ เสีย 5
ตอบ เราควรจะสั่งน้อยกว่า 200
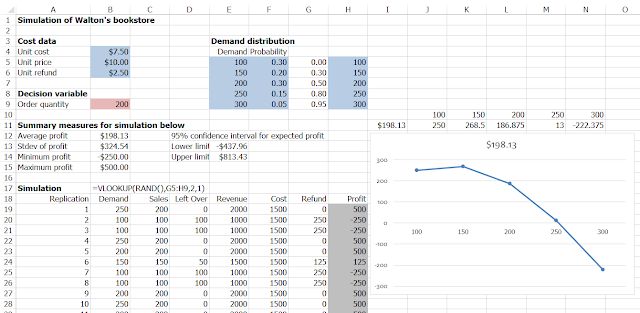
ทดลองสร้าง Simulation
ปริมาณ สั่ง x = 200
ขายได้ D = 180
ยอดขาย { = D ; x>D | = x ; x<D}
= MIN (x,D)
Profit = 10 MIN(D,X) - (7.5X) - 2.5(200-MIN(D,X))
ถ้าเราอยากรู้ ค่าเฉลี่ย Profit ห้ามนำ ค่าเฉลี่ยของ Demand มาหา จะต้องใช้ Simulation
ห้าม ทำ : 10 MIN(E[D],x) - 7.5X + 2.5(x-MIN(E[D],X)) = 500 !!! มันผิด
P(837)
อธิบาย เนื้อหา
Uniform Distribution
- ถ้า ความสูงเท่ากัน (Density) โอกาศที่จะได้ค่าในช่วง นั้นๆ จะมีค่าเท่ากัน
Rand() จะให้ Uniform ระหว่าง 0-1
RandBetween(20,30) จะให้ Uniform ระหว่าง 20 - 30
Discrete Distribution
จะต้องบอกค่าที่เปนไปได้ทั้งหมด รวมถึงความน่าจะเปนด้วย
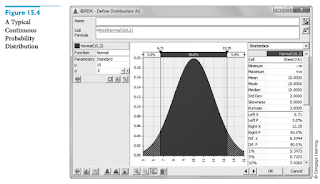
Normal Distribution
อธิบายไปแล้ว
Triangular Distribution
จะมีค่าสูงสุดต่ำสุด และ Most Likely เช่นจำนวนวันที่จะทำงานเสร็จ น่าจะประมาณกี่วัน
Density สูงๆ จะมีโอกาสเกิดสูง
Binomail Distribution ( Discrete)
เปน จำนวน success จากการทดลอง n ครั้งแต่ละครั้งมี โอกาศ success ด้วย Probability P
โจทย์ ตัวอย่างให้ทำ
15.1 Ski Jacket Production
ปรับ Weight คะแนน
40 - 40 - 20
To
25 - 40 - 35
ข้อสอบ Final
- Simulation ที่ทำวันนี้ ออก Uncetainty 1 ตัว แน่อนอน ออกเยอะ
จะคิดยอด Sell = MIN ( ที่ซื้อ , Demand ) ขายอย่างไร
ออกเรื่อง Card วันแม่ !!
- Expectation เช่น ให้ Demand มาเปน Discrete Distribution
หา Mean , STDev , หา Varience = E[X^2] - E[X]^2

ให้อธิบาย ถ้า Uniform นี้อยู่ในช่วง 1 - 30 ให้มัน map ไปที่ 100 อยู่ในช่วง x map ไป ที่ 250
อธิบาย ช่อง Sell = MIN( Demand, Order Q)
อธิบายเป็นช่อง ๆ
ตัดสินใจว่าจะเลือกผลิต อันไหน
- มีข้อยาก ไว้ตัด A โดยเอาไป ปนกับ ก่อนหน้านั้น พวก Optimization
? mass function ของ Binomial เราต้องสามารถ Generate Simulation แบบ Binomial ได้
################################ END 20150726 ##################################